특이값 분해 - SVD

SVD 는 정방행렬뿐만 아니라 행과 열의 크기가 다른 m * n 행렬도 분해 가능

 

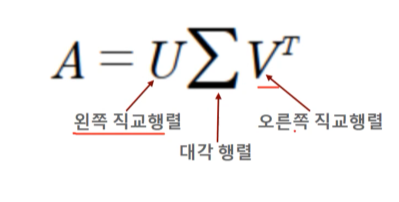
u와 v는 특이벡터다. 모든 특이 벡터는 서로 직교하는 성질을 가진다.

Σ 는 대각행렬이며, 대각성분이 행렬 A의 특이값이다.

 

 

Compact SVD : 행렬간 종속성이 높을때, 대각 행렬의 대각성분이 0이 많이 많아진다. 이때 분해가 compact 하게 되는 경향이 있다.

 

Tuncated SVD : 대각 원소 가운데 상위 r개만 추출하여 차원 축소

 

 

 

m * n = (m * r) * (r * r) * (r * n) 

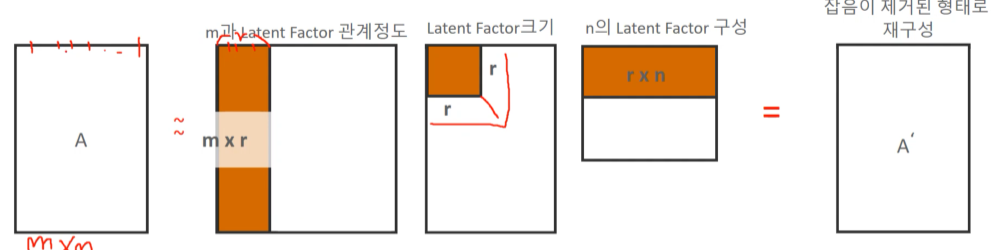
SVD는 차원 축소를 위한 행렬 분해를 통해 Latent Factor(잠재 요인)을 찾을 수 있는데 이렇게 찾아진 latent Facetor는 많은 분야에 활용(추천 엔진, 문서의 잠재 의미 분석) 

 

SVD로 차원 축소 행렬 분해된 후 다시 분해된 행렬을 이용하여 복원된 데이터 셋은 데이터의 손실이 불가피함

 

n이 1000차원인 행렬을 r=10으로 차원축소하면 굉장히 함축적으로 바뀜. 

 

원본데이터에 UΣ 를 적용하여 차원 축소

 

-이미지 압축/변환

-추천 엔진

-문서 잠재 의미 분석

-의사 역행렬을 통한 모델 예측