Score-Based Generative Modeling Through Stochastic Diffrential Equations
Diffusion 을 조금 더 이해하기 위해서 적어보는 글 2탄.

Introduction
새롭게 score 기반 생성모델이 정의된 후 diffusion 기반의 Denoising Diffusion Probablistic Model 이라는 논문이 나왔습니다. Score 기반 생성모델의 저자인 yang song은 이후 score 모델과 diffusion 기반 모델이 어떤 관계를 가지고 있는지 연구하였고 결론적으로는 같은 방식의 SDE(stochastic diffrential equation) 기반 방식이라는것을 발견하게 됩니다.
Preliminary
\begin{align} \frac{\mathrm{d}x} {\mathrm{d}t} = t, \end{align}
\begin{align} x = \frac{t^2}{2} + C \end{align}
\begin{align} \mathrm{d}x = f(x, t) \, \mathrm{d}t \end{align}
ordinary diffrential equation이란 t에 따라 변하는 x(t)를 구하기 위한 방정식 입니다.
\begin{align} \mathrm{d}x = f(x, t) \, \mathrm{d}t + g(t) \, \mathrm{d}w \end{align}
여기에 randomness 성질을 가진 뒷항을 추가하면 Stochastic Diffrential Equation가 됩니다.
- f(x, t) 항은 drift coefficient라 부르고 x(t)의 변화 추세를 보입니다.
- g(t)항은 diffusion coefficient라 부르고 랜덤성을 추가시켜줍니다.
- w는 Brownian motion을 나타내고 dw는 white noise, 즉 정규분포의 랜덤성을 가지는 항이라 봅니다.
- t의 범위가 [0, T] 라면 식의 해인 x(t)는 [0, T] 사이의 trajectories를 보입니다.
\begin{equation} \mathrm{d}\mathbf{x} = [\mathbf{f}(\mathbf{x}, t) - g^2(t) \nabla_\mathbf{x} \log p_t(\mathbf{x})]\mathrm{d}t + g(t) \mathrm{d} \mathbf{w}.\label{rsde} \end{equation}
SDE에는 그에 대응되는 reverse SDE가 반드시 존재합니다.
Perturbing data with as SDE
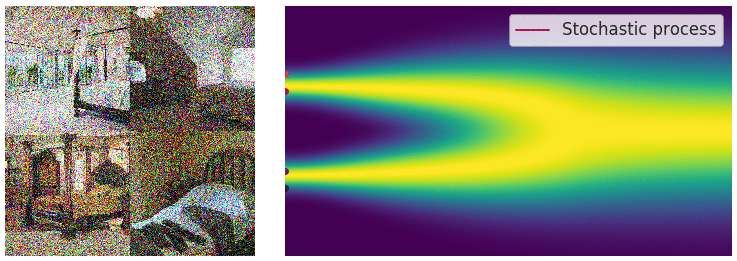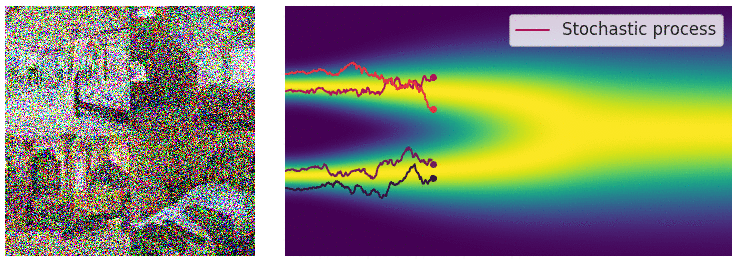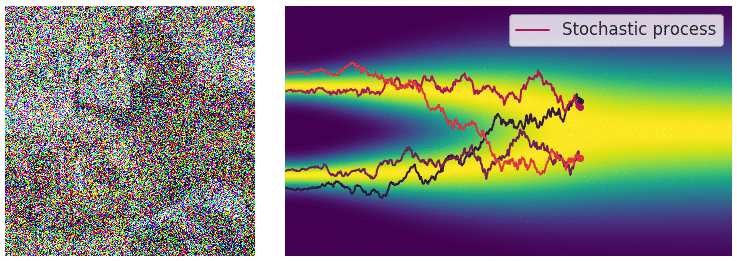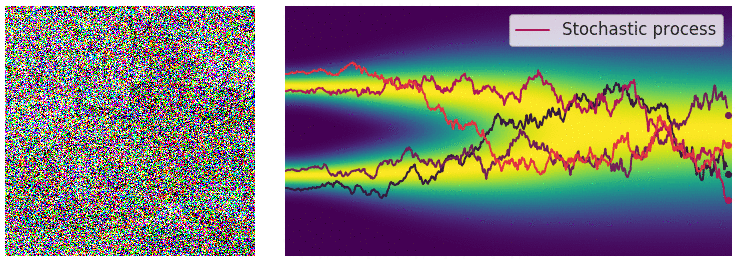
이전 SMLD(Generative Modeling by Estimating Gradients of the Data Distribution) 에서 우리는 단순하게 score를 matching하는것이 아니라 score를 denoising 시켜준 이후 score matching을 해준다면 밀도가 부족한 부분에 대해서도 score를 잘 학습시킬 수 있다는것을 알게되었습니다. 이후 본 논문에서는 이렇게 score를 넣어주는 과정을 다시 재조명했고 discretization된 SDE의 한 과정이라 보게 됩니다.
\begin{equation} \mathbf{x}_i = \mathbf{x}_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2} \, \mathbf{z}_{i-1}, \quad i = 1, 2, \dots, N. \end{equation}
\begin{equation} \mathrm{d}\mathbf{x} = \sqrt{\frac{\mathrm{d}[\sigma^2(t)]}{\mathrm{d}t}} \, \mathrm{d}w. \end{equation}
첫 식은 기존 방식데로 score에 노이즈를 추가시켜주는 과정입니다. 여기서 N을 무한으로 보낸다면 두번째 식처럼 SDE 방정식으로 전개시킬 수 있습니다. 즉 첫 식은 노이즈를 무한번에 가깝게 넣어주게 되면 SDE에서 drift항 없이 white noise항만 가지고 있는 식으로 볼 수 있습니다. 또한 위 식은 노이즈의 분산이 점점 증가하는 variance exploding 형태입니다.
\begin{equation} \mathbf{x}_i = \sqrt{1 - \beta_i} \mathbf{x}_{i-1} + \sqrt{\beta_i} \mathbf{z}_{i-1} \end{equation}
\begin{equation} \mathrm{d}\mathbf{x} = -\frac{1}{2} \beta(t) \mathbf{x} \, \mathrm{d}t + \sqrt{\beta(t)} \, \mathrm{d}w \end{equation}
여기서 봐야할점은 DDPM의 forward process에서 노이즈를 넣어주는식도 N을 무한으로 보낸다면 SDE로 볼 수 있다는 점입니다. 즉 score model이나 diffusion 모델이나 둘다 discretization된 SDE의 한 형태라고 볼 수 있습니다. score 모델과의 차이점은 노이즈가 유지되려고 하는 variance preserving 형태입니다.
Reversing the SDE for sample generation

score 기반 모델에서는 최종적으로 구한 score function을 Langevin dynamics에 넣어주고 샘플링함으로서 점차적으로 원래 분포에 가깝게 진행되었습니다. 본 논문에서는 위와 마찬가지로 reverse SDE와 Langevin dynamics가 같은 형태로 이루어져서 같은 역할을 한다고 주장합니다.

Langevin dynamics에 학습시킨 score를 넣어줬던것 처럼 reverse SDE에서도 학습 시켰던 score함수를 넣어주고 방정식을 풂으로서 점차적으로 원래 이미지를 생성해 나가는것을 볼 수 있습니다.
\begin{equation} \mathbb{E}_{t \in \mathcal{U}(0, T)}\mathbb{E}_{p_t(\mathbf{x})}[\lambda(t) \| \nabla_\mathbf{x} \log p_t(\mathbf{x}) - \mathbf{s}_\theta(\mathbf{x}, t) \|_2^2], \end{equation}
그리고 이전에 denoising score matching을 통해 score를 구했던것과 마찬가지로 여기서도 network를 통해서 score 함수를 학습시킵니다. 이것은 DDPM의 reverse process에서 unet을 통해 노이즈를 학습시키는것과 같은 모습입니다.
How to solve the reverse SDE
\begin{aligned} \Delta \mathbf{x} &\gets [\mathbf{f}(\mathbf{x}, t) - g^2(t) \mathbf{s}_\theta(\mathbf{x}, t)]\Delta t + g(t) \sqrt{\vert \Delta t\vert }\mathbf{z}_t \\ \mathbf{x} &\gets \mathbf{x} + \Delta \mathbf{x}\\ t &\gets t + \Delta t, \end{aligned}
reverse SDE는 어떻게 어떻게 풀 수 있을까요? 기존에 Langvevin dynamics의 해를 구할때 풀었던 방식처럼 Euler-maruyama 방식을 사용합니다. 연속적이고 stochastic한 방정식을 finite 하게 바꿔줌으로서 수치적으로 계산할 수 있게 됩니다.

여기서 rever SDE는 두가지 특별한 특징을 가지고 있습니다.
- $\nabla_\mathbf{x} \log p_t(\mathbf{x})$의 측정치를 오직 시간에만 의존하는 $s_\theta(\mathbf{x}, t)$를 통해 구할 수 있습니다.
- marginal distribution인 $\ p_t(\mathbf{x}) $ 로부터 샘플링 하는것에만 관심이 있는 상태입니다. 그리고 각각의 다른 time step에서 구한 샘플은 서로 연관도가 없기에 어떠한 trajectory도 생성하지 않고 독립적으로 샘플을 얻어도 되게 합니다. 즉 정확한 reverse SDE를 따르지 않기에 추가적인 fine tune을 적용해준 모습입니다.
이러한 두가지 특성으로 인해 저자는 MCMC 접근법을 reverse SDE 과정에 추가시킴으로서 fine tune하는 새로운 방법을 제안합니다. 저자는 이것을 Predictor-Corrector samplers 라고 지칭하는데, predictor는 numerical SDE solver이고 corrector는 score function에만 의존하는 Langevin dynamics 입니다. 즉 기존 numerical SDE solvers 방식에 MCMC 방법론을 껴넣음으로서 생플링 과정에서 더 정확한 예측 결과를 가질 수 있게 만듭니다.
Probability flow ODE
위와 같은 방법으로 좋은 품질의 샘플을 생성할 수 있게 됐지만 SDE와 MCMC 정확한 likelihood를 측정할 방법이 없습니다. 즉 우리가 만든 모델을 평가할 수 있는 평가지표가 없습니다. 그래서 저자는 정확한 likelihood를 계산할 수 있는 probability flow ODE를 제안합니다.
\begin{equation} \mathrm{d} \mathbf{x} = \bigg[\mathbf{f}(\mathbf{x}, t) - \frac{1}{2}g^2(t) \nabla_\mathbf{x} \log p_t(\mathbf{x})\bigg] \mathrm{d}t.\label{prob_ode} \end{equation}
기존 reverse SDE 식에서 뒷항을 제거한 ODE 버전으로 바꿔줌으로서 정확한 likelihood를 계산할 수 있게 되었습니다. 이렇게 식을 변환시켜줘도 같은 data distribution에 대한 결과를 가진다고 합니다. $\nabla_\mathbf{x} \log p_t(\mathbf{x})$가 $\mathbf{s}_\theta(\mathbf{x}, t)$로 대체되면서 probability flow ODE는 neural ODE의 특수한 경우라 볼 수 있습니다. 그래서 정확한 loglikelhood를 계산할 수 있다는 nueral ODE의 특징을 가지게 됩니다.

flow ODE로 바꿔준 결과로 노이즈에서 원래 데이터 분포로 가는 과정은 smooth하고 deterministic하게 바뀌게 됩니다. NSCN은 diffusion term만 있는 식이기에 기존 노이즈를 넣어주는 과정은 SDE로 진행하지만 노이즈를 제하는 과정에서 ODE flow로 바꿔서 계산해주는것 같습니다.
Controllable generatior for inverse problme solving
마지막으로 저자는 생성을 할때 조건을 넣어주는 방법을 제시합니다. score-based model은 inverse problems를 푸는데 적합한 방법론입니다. 왜냐하면 inver problems가 Bayesian inference problems와 같기 때문입니다.
만약 우리가 $\mathbf{x}$, $\mathbf{y}$ 라는 두가지 변수를 알고있고 $p(\mathbf{y} \mid \mathbf{x})$ 있다고 가정해봅니다. 그렇다면 그에 해당하는 invers problems는 $p(\mathbf{x} \mid \mathbf{y}) = p(\mathbf{x}) p(\mathbf{y} \mid \mathbf{x}) / \int p(\mathbf{x}) p(\mathbf{y} \mid \mathbf{x}) \mathrm{d} \mathbf{x}$를 구하는것 입니다. 이때 양변에 x에 대한 미분을 취해보겠습니다.
\begin{equation} \nabla_\mathbf{x} \log p(\mathbf{x} \mid \mathbf{y}) = \nabla_\mathbf{x} \log p(\mathbf{x}) + \nabla_\mathbf{x} \log p(\mathbf{y} \mid \mathbf{x}).\label{inverse_problem} \end{equation}
이때 $\mathbf{s}_\theta(\mathbf{x}) \approx \nabla_\mathbf{x} \log p(\mathbf{x})$ 이기에 첫항에 대해서 알고있고 두번째 항은 우리가 알고있다고 가정했기에 결국 $p(\mathbf{x} \mid \mathbf{y}) $를 Langevin dynamics를 통해 갱신해 나감으로서 inverse problems를 풀 수 있게 됩니다.

Take home message
- 저자는 score-based model과 diffusion 사이 연관성을 찾고 결국 SDE 관점에서 봤을때 같은 방법임을 보입니다.
- 기존 noise 추가해주는 과정을 무한에 가깝게 넣어줌으로서 SDE 관점에서 볼 수 있고, SDE Solver 방식으로 문제를 풀 수 있게 합니다.
- Probability flow ODE로 바꿔주면서 계산을 더 간단하게 만들었고, likelihood 평가를 할 수 있게 해줍니다.
- score based model은 inverse problem을 풀기에 적합하기에 같은 방법인 ddpm도 condition을 넣어줘서 inverse problem을 풀 수 있게 해줍니다.
Reference
https://dlaiml.tistory.com/entry/Score-Based-Generative-Modeling-through-Stochastic-Differential-Equations
https://yang-song.net/blog/2021/score/#mjx-eqn%3Arsde
https://www.youtube.com/watch?v=uG2ceFnUeQU
모르는것 :
MCMC란?
Langevin dynamics와 Euler-maruyama 방식이란?
neural ODE, normalizing flow란?
https://www.youtube.com/watch?v=wMmqCMwuM2Q 나중에 참고해보기
reverse sde와 langevin dynamics의 정확한 차이