로지스틱 회귀는 시그모이드 최적곡선을 찾는다. 마법의 확률곡선. 실수값을 확률값으로 변환해주는 활용도가 높은 함수다. 시그모이스 함수의 최적선을 찾고, 이 시그모이드 함수의 ㅂ나환값을 확률로 간주해 확률에 따라 분류를 결정한다. 이름은 회귀지만 분류에 사용된다.
로지스틱 회귀는 주로 이진분류에 사용된다. 반환된 예측값을 예측 확률을 의미한다. 반환된 예측 확률이 0.5 이상이면 1로, 0.5 이하이면 0으로 예측한다.

단순 선형 회귀 : y=w1x + w0
Odds(p) = p/1-p
로그 오즈를 이용한 회귀분석 식
Log(odds(p)) = w1x + w0
p(x) = 1 / 1+e^-(w1x+w0)
로지스틱 회귀는 학습을 통해 시그모이스 함수의 w를 최적화하여 예측한다.
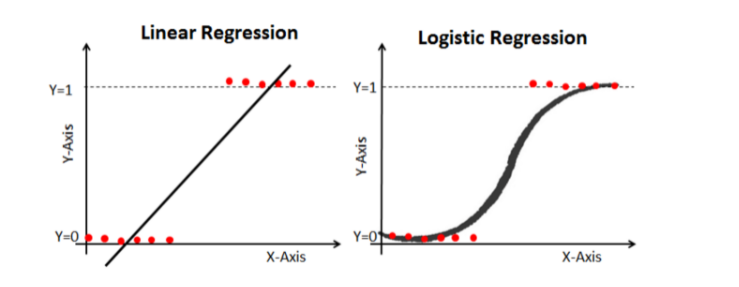
선형회귀는 로지스틱 회귀만큼의 분류는 어렵다.
로지스틱 회귀는 가볍고 빠르고, 이진분류 예측 성능도 뛰어나다. 로지스틱 회귀를 이진분류의 기본모델로 사용하는 경우가 많다. 로지스틱 회귀는 희소한 데이터세트 분류에도 뛰어난 성능을 보인다.
LogisticRegression 클래스를 이용한다. 주요 하이퍼 파라미터는 penalty와 C가 있다.
penalty는 규제의 유형을 의미하며 L1규제와 L2규제가 있다
C는 규제 강도인 alpha의 역수이다. c값이 작으면 규제 강도가 크다
https://soobarkbar.tistory.com/12
참고하면 원리를 좀더 알수 있다.
'머신러닝 > 인프런' 카테고리의 다른 글
| 차원 축소(PCA만) (0) | 2021.07.11 |
|---|---|
| 회귀 트리 (0) | 2021.05.16 |
| 선형 회귀 모델을 위한 데이터 변환 (0) | 2021.05.15 |
| 라쏘 회귀 (0) | 2021.05.15 |
| 회귀 (0) | 2021.03.28 |