tree : 노드들의 집합체, 계층적인 관계, 어떤 정보는 노드에 포함된다. 뿌리 노드가 존재한다.

루트를 제외한 각각의 노드는 정확하게 하나의 노드를 부모노드로 가진다.
degree : 노드가 가지고 있는 자녀의 숫자 ex) E의 degree는 2
sibling : 같은 부모를 가지는 노드들 ex) j k l 은 I라는 같은 부모노드를 가진다.
leaf : 자녀가 없는 degree 0인 노드들
internal : 자녀가 있는 노드
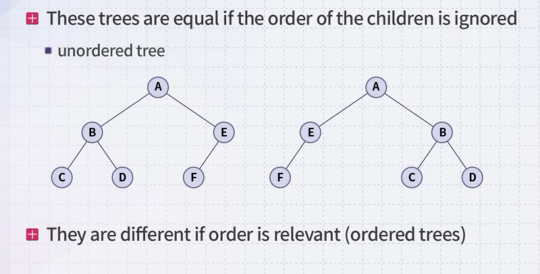
unordered : 자녀의 순서가 무시되는
ordered : 자녀의 순서를 지켜야하는
트리의 경로를 정한다고 하면 부모와 자식 노드간 관계에서 부모 노드가 무조건 앞으로 와야하며
경로의 길이는 선의 갯수이다. 노드의 갯수가 아니다.
어떤 한 노드와 루트사이의 경로는 유니크하다.
뎁스 : 루트 노드로부터 해당 노드까지의 경로의 길이. ex) 위 사진에서 D의뎁스는 2
height : 어떤 트리의 가장 큰 뎁스.
만약 트리에 노드가 루트노드 하나밖에 존재하지 않으면 height는 0이다. 뎁스가 0이기 때문이다.
만약 트리가 텅텅 비어있으면 루트도 없으므로 height는 -1이다.
ancestor : 노드 A에서 노드B가지의 경로가 존재한다고 하면 A는 B의 ancestor다
descendant : B는 A의 자손이다.
트리에서는 자기 자신은 자기 자신의 자손이다. A부터 A까지는 길이가 0인 경로다.
strictly descendant : 자기 자신이 자기자신의 자손이나 부모가 되는것을 금지. 일반적으로는 안쓰임
트리는 실제로 우리가 어떻게 자료구조를 포현할까라고 하면, 자녀노드들의 list representation을 많이 사용한다.
linked-list 같은것을 사용한다.

그래프 : 어떤 데이터 사이의 인접한 정보를 저장하는 자료구조
object : 저장하고자 하는 객체. 어떤 사람, 어떤 도시. 오브젝트를 표현하는 노드를 vertex라고도 표현.
relationship : object간 관계. edge로 연결시킴. arc나 link라고도 부름.

undirected graph : 방향이 없는 그래프. 엣지간의 순서가 없음. adjacency matrix나 adjacency list를 쓸 수 있다.
v1과 v2의 엣지가 {V1, V2}로 표현되어 있고, v1에서 v2로 가는 엣지, v2에서 v1으로 가는 엣지가 모두 있다. 자기 자신에서 자기자신으로 가는 엣지가 없다고 가정해보자. 최대한 많은 엣지의 갯수는 vC2 이다.
degree : 자신의 이웃 벌텍스의 갯수.
neighbor : 하나의 엣지로 곧바로 갈 수 있는 관계인 vertex

서브 그래프 : 오리지널 그래프에서 엣지와 vertex들을 추출해냈을때, 추출해낸 그래프
경로 : 몇 개의 엣지를 거쳐갔는가. 몇개의 vertex들로 이루어져있는가가 아니다.
trivial path : length가 0인, 자기자신에 머물러 있는것
simple path : 경로상에 처음 vertex와 마지막 vertex를 제외하면, 경로안에 중복이 없을때를 칭한다.
A-B-C-A 는 simple 하지만 A-B-C-B-A는 simple 하지 않다.
simple cycle : simple path이면서 처음과 마지막 vertex가 같은 경우

connectedness : 두 vertex와 connect 되어있는것은 그 사이에 경로가 있다는 것을 말한다.
그래프가 connected 되어 있다는것은 무작위로 고른 두 노드간 경로가 있는것인데, 우측 그림은 경로가 없는 노드들도 있으므로 connected 되어 있지 않다.

Weighted graph : 엣지가 단순히 연결성만을 표현하는것이 아니라, 연결되어있고 이들 사이에 어떤 숫자나 값을 부여한 것을 얘기한다. 부여되는값은 거리 같은것을 예로 들 수 있다. ex) 대전과 수원 사이의 거리, A에서 B까지 가는데 드는 비용
경로 : 경로간의 수치가 정해졌는데 그것을 더한다. ex) A-D-G 경로 길이는 8.8. 같은 출발지 같은 목적지라도 경로 길이가 달라질 수 있다. shortest path에 관해 생각해 볼 수 있다.
tee도 그래프의 한 종류라고 얘기할 수 있다. 그래프가 트리가 되려면 일단 이 그래프가 connected되어 이썽야하고, 모든 vertex간에 경로가 있어야 하며, 그 경로는 유니크해야한다.
ㄴ트리에서는 반드시 엣지의 개수가 노드의 개수보다 하나가 적다.
트리는 사이클이 존재하지 않는다. 주어진 트리에 하나의 엣지를 추가하면 그 트리는 반드시 사이클이 된다.
하나의 엣지를 제거하면 트리는 disconnected 되고, 두개의 트리가 된다.
Forest : 트리들의 집합. 트리의 정의에서 ceooectedness의 constraint를 제거. 어떤 그래프가 포레스트라고 하면, 사이클이 없다고 하면 포레스트가 된다.
vertex 개수가 edge개수보다 항상 많다. 트리의 개수를 구하고 싶으면, vertex 개수에서 edge 개수를 빼면 트리의 개수를 구할 수 있다.
포레스트에서 하나의 엣지를 제거하면, 트리를 하나 더 만들게 되는 효과가 있다.
Directed graph : v1과 v2 엣지가 있다하면 양방향으로 갈수 없고 한 방향으로만 갈 수 있는 그래프. degree가 두 종류로 나뉘어진다.
in_degree : 나로 들어오는 엣지의 갯수
out_degree : 나로부터 출발하는 엣지의 갯수
source : in_degree가 0인것.
sink : out_degree가 0인 vertex
path : 방향성을 고려한 경로가 존재해야한다.
stronly_connected : 방향성을 인정했을때 모든 pair간에 경로가 존재함. 무작위로 고른 u와 v에 대해서 u에서 v까지 방향 경로와 v에서 u까지 방향 경로 둘다 존재한다.
weakly_connected : 방향성을 무시하고 연결성을 따졌을때 그래프가 연결. u에서 v까지나 v에서 u까지 어느 하나의 경로만 존재한다.
weighted_directed_graph
directed acyclic 그래프 (DAG) : 방향이 있으나 사이클이 존재하지 않는 그래프. edge에 direction이 있지만 사이클이 존재하지 않는 경우. 순서를 정할때 사용되는 그래프의 형태

binary-relation list : edge들을 쭉 나열해 놓은 것. 이것을 저장하기 위해서는 edge 개수만큼의 메모리가 필요하다. 두 vertex 사이에 엣지가 존재하는지 보려면, 이 엣지들을 하나씩 하나씩 보면서 우리가 찾고있는 엣지가 있는지 확인해야한다. 두 vertex사이가 연결되어있다 아니다를 체크하기 위해서는 최대 엣지갯수만큼의 프로세싱을 해야한다. 어떤 vertex 하나로부터 neighbor를 구하고 싶을때도 마찬가지로 도는 엣지들을 하나씩 하나씩 체크해야하기 때문에 비효율적이다.

, adjacency matrix : 메로리를 가장 많이 쓰는 표현법이다. v제곱개만큼의 메모리가 사용된다. v5의 neighbor를 구하고 싶으면 V5 즉 위 그림의 5번째줄의 원소를 다 봐야하기 때문에 vertex 갯수 만큼을 봐야하는 computational overhead 가 있다. v1과 v2사이의 엣지가 있냐 없냐 판별은 한번이면 되므로 가장 효율적이다. weighted 그래프를 표현하고 싶다고 하면, 각각의 cell에 True/False 가 아니라 weight 값 자체를 입력해 주면 된다.
adjacency list : 일반적인 알고리즘에서 가장 많이 사용하는 그래프의 표현법. 각 노드들을 기준으로 자신과 연결되어 있는 엣지가 있는 vertex들을 리스트로 표현하는 형태. 메모리 요구량은 전체 vertex 갯수만큼의 linked list가 필요하고, 전체 데이터 개수를 따져보면, 엣지의 개수를 넘어가지 않는다. 최대 vertex 혹은 edge 갯수만큼의 메모리를 요구
reference
http://www.kmooc.kr/courses/course-v1:SKKUk+SKKU_46+2021_T1/courseware/1158909c057347478d7386a2b7e97214/bf6440dd5a3c4fbc96285eab636931f6/?child=first
'자료구조 및 알고리즘 > k-mooc' 카테고리의 다른 글
| 최소신장트리 알고리즘 (0) | 2021.08.31 |
|---|---|
| 힙 자료구조 (0) | 2021.08.24 |
| 점근적 분석 (0) | 2021.08.01 |
| 그래프 탐색 알고리즘 (0) | 2021.07.25 |
| 선형 자료 구조 (0) | 2021.07.16 |