lecture 11에서는 novel view synthesis 특히 NeRF에 관한 부분에 대해서 다뤘다. 이번 강의에서는 NeRF가 발전한 방향에 대해서 간단하게 다루고, 3dgs를 렌더링 관점에서 설명한다.
9강 10강의 path tracing과 BRDF 모델링 부분은 정확히 이해하지 못했다. 지금 나에게는 필요하지 않아서 미래의 나에게 맡긴다.

NeRF는 3d 공간좌표와 보는 방향을 입력으로 받아 색깔과 density를 구해내는 방식이였다. InstantNGP는 NeRF를 발전시켜 모든 3d 포인트들에 대해서 고려하려면 시간이 오래 걸린다는 문제를 해결하려는 기법이다. 3d 공간을 hashing을 통해 lookup feature table로 변환하여 저장한다. 즉 메모리 사용을 높혀서 미리 공간상 점에 대한 정보를 저장해놓고, 나중에 불러올때 시간을 절약하려는 방식이다. 저장된 feature lookup은 이후에 선형보간을 통해 decoding되고 보는 방향 정보와 concat되어 뉴럴 네트워크에 입력된다. 이때 3d 복셀의 해상도를 여러개로 둘 수 있는점을 고려하여 색깔에 따라 크기가 다른 hashing이 된다.

TensoRF는 3d 공간상의 점을 렌더링에 바로 활용하려면 시간이 오래걸리는점을 고려하여 3d 공간을 여러 평면과 축의 조합으로 표현하려는 방법이다. 이 방법도 InstantNGP와 마찬가지로 시간복잡도를 낮추기 위해 메모리 사용량을 높히는 방법이다. 공간상 점을 위와 같은 방식으로 나누어 표현하면 시간복잡도가 O(N^3)에서 O(3N^2)이 된다.


아직 읽어보지 못한 논문들이라 패스하지만 꼭 읽어보자.
3D Gaussian Splatting

3d 가우시안들을 공간상에 흩뿌려놓고 NeRF와 마찬가지 방식으로 보는 스크린 방향으로 투영시키면서 렌더링 하는 방식이다. NeRF는 공간상의 point cloud들을 고려하지 않고 ray를 sampling 하는 과정이 포함되어 시간이 오래걸렸지만, 3dgs는 colmap 결과로 나온 point cloud들을 explicit 하게 활용하면서 inference에서 상당한 시간 단축을 할 수 있었다. 또한 3dgs는 뉴럴넷을 쓰지 않기에 메모리 효율도 비교적 좋다. Explicit한 point cloud 3d representation을 사용하기에 기존 컴퓨터 그래픽스 렌더링 방식에 접목시키기 적합하다.
3dgs의 시초는 point-based rendering이다. 공간상의 점들을 각각의 eppilsoidal volume으로 취급한다. 3dgs로 본격적으로 들어가기 앞서 point-based rendering을 잠시 알아보자.


3d mesh를 representation으로 활용하던 과거 시절, mesh보다 더 작고 간편하게 활용할 수 있는 방법에 대해서 연구자들은 찾고 있었다. 또한 3d laser scanning의 발달로 인해 조형물을 point cloud로 얻어올 수 있게 되었다. Point cloud를 일일히 mesh로 변환하는것은 시간이 너무 오래 걸리기에 point cloud 자체로 렌더링 활용하는 방법에 대해서 연구가 시작되었다.

물질의 표면은 여러 점들의 합으로 표현할 수 있다. 표면의 geometry와 reflectance등을 표현할 수 있다. 점 사이간 연결성과 텍스쳐를 저장하지 않아도 된다는 장점이 있다.


Surfel은 surface element의 줄임말이다. 지금부터 표면의 작은 영역을 surfel이라 부르도록 하자. 그리고 surfel은 위치와 색을 가진 point cloud로 표현할 수 있다. Points 사이 빈 표면에 대해서는 두 point를 interpolate 하면서 표현할 수 있다.
또한 point cloud가 위치와 색만 가졌다고 생각하는게 아니라 Normal, Raidus 정보를 포함시킬 수 있다. 이때 surfel은 단순 point cloud 형태가 아니라 disk 형태가 된다.


Sufel을 활용하여 diffrentiable rendering 하려는 방법론들도 발전해왔다. Surfel을 공중에 흩뿌리고 렌더링하는 과정을 미분가능하게 만듦으로써 surfel요소를 뉴럴 네트워크에 담아서 forward하고, 렌더링 사이 결과 loss를 구하여 backward하는 딥러닝 방법론과 연결시킬 수 있게 되었다. 또한 Surfel을 흩뿌리는 방법이 아니라 3d volume을 공간상에 흩뿌리는 방법도 발전되어왔다. Volume을 흩뿌릴시 장점은 단순 z-buffer 방식으로 깊이값이 가장 가까운 요소만 렌더링에 활용하는것이 아니라 opacity 요소를 고려할 수 있게 된다. 즉 색을 가진 입자를 섞어서 표현할 수 있게 된다.

Splat 방식은 공중에 입자를 미리 뿌려놓을수 있는 장점이 있다. NeRF에서는 screen위의 가로 세로 픽셀을 고려하여 픽셀마다 ray를 쏴서 점을 sampling 하는 과정이 필요했다. 그러나 splat 방식을 활용하면 그러한 과정이 필요없을뿐만 아니라, point cloud를 뽑아내는 colmap 기술을 활용할 수 있게 된다. 그렇게 뽑아낸 point cloud는 기존 컴퓨터 그래픽스 파이프라인인 local-world, world-cam 변환, rasterization 과정을 활용할 수 있게 된다.



이제부터는 2d surfel이 아니라 3d 타원형 gaussian volume을 생각하게 된다. 각각의 gaussian은 opacity, color, 중심점, 공분산 요소를 가지게 된다. 3dgs에서 가우시안 분포 공식은 기존 가우시안 분포 공식을 다변수 형태로 바꾼것이다. 3d 공간상에서 x, y, z에 대하여 어떻게 퍼져있는지를 표현한다는 관점에서 kernel이라 부르고, 공분산이라는 요소를 사용한다.
가우시안의 공식을 살펴보면 (x-p)^2 꼴로 되어있는것을 볼 수 있는데, 공간상의 가우시안 점 p가 투영될 픽셀상의 점 x에 얼마나 영향을 미치는지로 모델링 한것이다. 그리고 이때 분모에는 공분산이 들어간다. 이 강의에서 설명되지 않았지만 공분산은 특이값 분해로 방식으로 rotation행렬과 scale행렬의 곱으로 표현할 수 있다. Scale은 특이값 형태로, rotation 값은 특이벡터 형태로 표현되는것 같은데 나중에 다시 포스팅 해보려고 한다.


colmap에서 얻은 pcd들을 정규화하여 object 좌표계로 생각한다. 이후 modelview transform과 projective transform을 거쳐서 ray 좌표계로 바꾸고, 이것을 alpha compositing 하여 볼륨 렌더링 공식에 사용한다. 사실 애매한 부분이 colmap의 결과는 wolrd 좌표계로 알고있는데, 왜 이것을 정규화하여 object 좌표계로 만든 뒤 camera 좌표계로 바로 바꿀수 있는지 이해가 잘 안간다. cudarasterizer 코드 에서 transformmatrx4x3( ,viewmatrix) 부분인것 같은데 이 viewmatrix가 정확히 어떤 변환을 의미하는지 이해하지 못했다.


Object 좌표계에 있던 가우시안들은 model-view 변환 통해서 x'으로, projective 변환 통해서 x''으로 변환된다. 여기서 추가 설명을 하자면 EWA splatting 2002에 따르면 model-view 변환은 rotation 변환과 translation 변환의 조합이므로 일반적인 선형변환이지만, projective 변환은 선형변환이지 않다. 그래서 우리는 이 projective 변환을 taylor expansion을 통해 1차 근사까지만 하여 표현하고, 이 1차 변환만을 가우시안에 적용시킨다.
또한 강의에서 유의할점으로 우리가 정하는 gaussian 커널의 중심점과 공분산은 object 좌표계 기준으로 설정한다.
이제부터는 지금까지 explicit 하게 정한 가우시안들을 어떻게 볼륨 렌더링에 적용할지를 생각한다.


우리는 object 좌표계에서 미리 ray 좌표계까지 변환하여 어떤 가우시안이 어떤 픽셀에 영향을 미치는지 어떤 순서로 나열되어있는지 알고 있다고 가정한다. 이후에 총 opacity σ(z)는 ray 좌표계 상에 모든점들의 가우시안값과 그 가우시안에 해당하는 opacity 값들의 가중합으로 표현된다. 마찬가지로 총 c(z), σ(z) 도 각각의 가중합으로 표현된다.

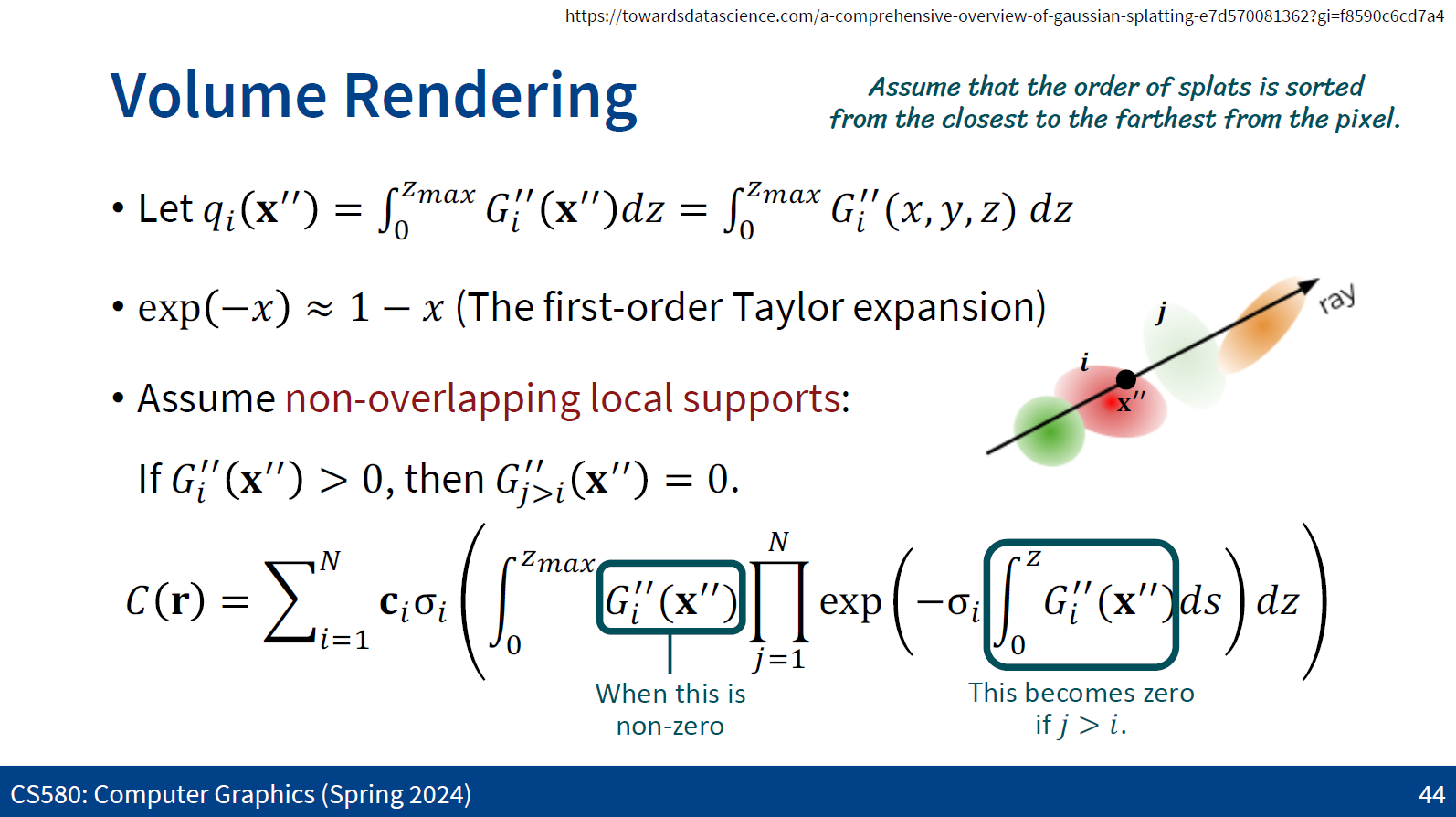

볼륨 렌더링 공식을 변형시켜 정리하면 맨 위 페이지 처럼 된다. 이때 식을 간단하게 변형시키기 위해 G''(x'')값들의 가중합을 q로 표현하고, non-overlapping 가정을 해본다. 또한 exp(-x)는 테일러 1차 근사에 의해 1-x로 표현한다. Non-overlapping은 표현하려는 가우시안 앞에있는것들만 고려하고 그 뒤에 있는것들을 무시하자는 것이다. 즉 C(r)을 표현하기 위해 ray상에 N까지의 모든 점들을 alpha compositing 하는데, 특정 z점에서 가우시안의 색값은 그 뒤에 있는 값들을 무시하는것이다. 이렇게 하면 품질을 떨어트리지 않는선에서 계산상의 이득을 얻을 수 있다.


그러면 G의 가중합인 q를 어떻게 계산할 수 있을까? 각각의 변환에 대해서 정의를 하고 미리 적용해두면 된다. Object 좌표계에서 camera 좌표계로의 변환은 선형변환으로 계산할 수 있다.


object 좌표계에서 정의된 p와 v는 카메라 좌표계로의 변환으로 인해 p'과 v'으로 바뀐다. 또한 3dgs의 공식에 좌표계 변환 식을 대입하면 상수 c' 항은 W의 절대값으로 계산되서 나온다. 여기서 헷갈렸던 점은 우리는 p 라는점이 object space에 정의되어있으므로 정방향으로 계산해야하고 코드상에서도 정방향으로 계산되어있는데, ppt에서는 대수적으로 좌표계 상의 변환을 나타내려 하므로 역변환으로 나타낸 점이다.


camera 좌표계에서 ray 좌표계로의 변환은 선형변환이 아니다. 따라서 원래의 perspective 변환을 taylor 근사화를 통해 1차식까지만 근사화하여 선형식으로 표현하려고 한다. 의미상으로는 변환을 1차까지만 근사하므로 가우시안의 중심점 p 근처에서의 변화만이 정확하게 표현된다. 그러나 이것은 가우시안 중심점에서 영향받는 픽셀 거리가 멀어질수록 오차가 늘어나는 단점이 있다. 테일러 근사를 위해 p'에서 1차 미분을 계산하면 결과가 다음과 같이 나온다.


g(x')은 x'에 대하여 1차 미분 즉 자코비안 항으로만 생각하고 나머지 뒤의 항은 무시한다. 이렇게 설정하면 ray 좌표계에서의 v''은 camera 좌표계의 v'에 앞뒤로 자코비안 항이 곱해진다.


최종적으로 우리는 object coordinates 상에 있던 p, V를 정규화 항을 곱해주면서 p''과 v''으로 표현할 수 있게 되었다. 가우시안 스플래팅의 렌더링의 과정은 다음과 같다.
1) 각각의 픽셀에 대하여 어떤 가우시안이 영향 미치는지 미리 계산하고
2) 깊이에 따라 sort 하고
3) 위에서 했던것과 같이 p'', v'', c를 각각 계산한다.
4) 마지막 그것들에 대하여 alpha compoisiting을 하여 렌더링 한다.

학습에 관한 과정은 다음과 같다.
1) sfm colmap을 통하여 각각의 pcd와 camera parameter를 미리 계산하고 그것들로 가우시안 splat을 미리 초기화한다. 또한 각각의 splat에 대하여 공분산을 설정한다.
2) loss를 구하여 splat parameter들을 덥데이트 한다.
3) clone 하고 split 한다.
3dgs는 딥러닝과 관련이 없다. 순수 그래픽스에 가까운 방법론이다. 12강까지 들으면서 렌더링 방법론을 간단하게 맛보고 어떻게 최신 방법론까지 발전되어 왔는지 흐름을 볼 수 있어 좋았다. 나중에 시간이 남으면 과제인 path tracing도 구현해보도록 하자.
아직 3dgs에 관해서는 강의 내에서 설명되지 않은 부분이 많은데,
sfm과 adaptive density control, 16x16 타일로 나누면서 병렬화 하여 쿠다 계산, 가우시안을 복사하여 픽셀별로 할당하고 깊이별로 할당하는 방법 등등..
이후에 시간이 남으면 code flow와 함께 봐보도록 하자..
reference :
https://mhsung.github.io/kaist-cs580-spring-2024/
CS580 Computer Graphics (KAIST, Spring 2024)
CS580: Computer Graphics Time & Location Time: Mon/Wed 10:30am - 11:45am (KST) Location: Online via Zoom Zoom Link Description This course covers advanced topics in computer graphics, focusing on rendering. It is divided into three parts: a review of basic
mhsung.github.io
'딥러닝 > 3D' 카테고리의 다른 글
| CS580 lecture 11 (0) | 2025.04.30 |
|---|---|
| Epipolar Geometry (0) | 2024.08.05 |
| Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains (리뷰) (1) | 2024.08.04 |